What is Infinity?
Infinity is a concept or idea that is boundless and endless.
Consider the Infinite Hotel or Hilbert’s Hotel:
The infinite hotel is a hotel with infinite rooms and infinite guests, meaning that every room is occupied. One day, a new guest arrives at the hotel and wants to get a room. The manager decides to accommodate this new guest by telling everyone in the hotel to move one room down. The guest in room 1 moves to room 2, the guest in room 2 moves to room 3, and so on. This leaves exactly one new room for the guest, that being room 1.
Why would we make everyone go through the hassle of moving to the room next to them, instead of just moving the person at the end?
With infinite rooms, it would be impossible to find a room for that person as there is no end to the number of guests and the number of rooms.
The next night, infinite new guests want to stay at this hotel. How would you accommodate these infinite guests?
Here’s how the manager did it: The manager tells everyone to move to the room that is double their room number. So the room 2 guest moves to room 4, the room 3 guest moves to room 6, and so on. If you write this down, you’ll quickly see a pattern. The rooms that are vacant are the ones that are odd. There are infinite odd numbers and therefore these new infinite vacant spots accommodate for the infinite new guests.
Consider a Circle:
Why are wheels shaped as a circle?
If your bicycle had a square shaped wheel, your ride would be pretty bumpy. If you increased the number of sides, such as a pentagon, your ride would become less bumpy. As you add more sides, the ride becomes smoother. What if we had infinite sides? With infinite sides, that would form a circle. Notably, a circle has no sides or corners, adding an interesting twist to the concept of infinity.
Sizes of infinities:
This section will investigate the size of infinities, but first, here are a few concepts to know before understanding sizes of infinities:
- A set is a collection of objects. For example, {1, 2, 3, 4, 5, 6} is a set, and {apple, pear, banana, broccoli} is also a set.
- In terms of infinite sets, can you think of any?
- Natural numbers, real numbers, integers, even and odd numbers are all infinite sets.
- One-to-one correspondence: How can you tell if the sizes of sets are the same?
- Matching each element in Set 1 to each element in Set 2 without having extra elements means that the size of the sets are the same.
- For example, if one set contains objects that are pineapples, and another set contains objects that are dragon fruit, by one-to-one correspondence, you can match a pineapple to a dragon fruit to create as many pineapple-dragon fruit pairs as possible. If there is no leftover pineapple or leftover dragon fruit, then these sets are equal in size.
How can we apply one-to-one correspondence to infinite sets? In other words, how can we compare the sizes of infinite sets to one another?
Natural Number Infinite Set Compared to Integer Infinite Set:
Natural numbers and integers are both infinite sets. Let’s try to compare the sizes of the natural number infinite set and integer infinite sets. As mentioned earlier, we can use one-to-one correspondence. So if each object in the natural number set matches each number in the integer set, then these sets are equal in size. Here’s how we could do this:

The list would go on for infinity. This conclusion of the natural and integer number sets isn’t intuitive. How could their set size be the same? Integers encompass negative numbers, positive numbers and zero while natural numbers only contain positive numbers and zero. However, when thinking about these infinite sets, we must remember that infinity is not an amount and it is endless. Therefore, even though it seems that there are many more integers, because they are both infinite and because of one-to-one correspondence, their infinite sets are the same size.
Natural Number Infinite Set Compared to Real Number Infinite Set:
Is the real number infinite set the same size as the natural number infinite set?
When looking at real numbers, we can narrow down our
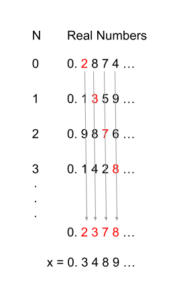
scope to all the real numbers between 0 and 1. As mentioned previously, we need to use one-to-one correspondence to show whether the infinite sets are of the same size. In other words, we need to see if we can match our natural numbers to real numbers. First, we can just simply choose a couple real numbers that are in between 0 and 1 (the numbers chosen do not matter and you can try this at home):
As marked in this photo, the second digit of the first line is marked, then the third digit of the second line, and so on.
The arrows point down where x = 0.3489. x is formed by simply adding 1 to each digit. So in the first line with the second digit of 2, we add one to get three which we place as the first digit after the decimal. We continue adding one, so the 13 turns into a 4, the 7 into a 8, and so on. This resulting number, x, is a new real number. This is because it is not the same as any of the lines. Because it takes one digit from each line and changes that digit, it will not be the same as any of the lines and therefore, it will be a real number that has not been listed.
So when we list these real numbers and try to match them to a natural number, {0, 1, 2, 3, 4, …}, we will find that not every real number will be ever listed, because there can always be a new real number that is formed. Therefore, there is no one-to-one correspondence. Finally, this shows that the real numbers infinite set and natural number set are different size infinities.
If you found this topic interesting or you would like to explore it some more, I really recommend the sources I looked at to write this post. Many of the sources explain what I talked about in greater depth and clarity, with much more credible sources. Thank you for reading and have a great week!
Sources:
- What is Infinity?
- Mathematician Explains Infinity in 5 Levels of Difficulty | WIRED
- Why Some Infinities are Larger than Others | Cantor’s Paradise
- Netflix Documentary: A Trip To Infinity
- Mathematicians Measure Infinities and Find They’re Equal | Quanta Magazine.
- Infinity and its cardinalities
- Strange but True: Infinity Comes in Different Sizes – Scientific American
- Integers & Reals have different, infinite sizes! **Cantor Diagonalization**

