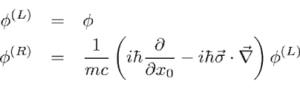Introduction
Should we describe our universe in classical terms or quantum terms? This question has sparked a lot of debate and the correct answer varies drastically depending on who you ask. But what if we could find the perfect middle? A way to describe our world with a mix of classical and quantum physics. This is called Quantum Field Theory (QFT). QFT is the blanket term used to describe the theories that combine elements of quantum mechanics with those of relativity and that aim to describe the interactions and behaviors of subatomic particles and force fields.
Arguably one of the most precise and successful QFTs is quantum electrodynamics (QED). QED was the first QFT developed and its aim is to mathematically describe interactions of charged particles with themselves, with the electromagnetic field and light with matter. The theory’s foundation is the idea that there is not a continuous field but instead charged particles interact by the exchange of virtual photons. These photons are called virtual because they cannot be seen or detected as that would violate conservation of energy and momentum. The exchange of photons is a “force”. This idea of virtual particles has also been carried over into other theories that deal with fundamental interactions of matter.
QED has a rich history, effective and simple mathematics, and a plethora of useful applications.
History
In 1925 Paul .A.M. Dirac, an English physicist, read a paper by Werner Heisenberg that initiated the change from the Bohr atomic model to a new idea, quantum mechanics. This led him into his fascination with the quantum world and in 1926 Dirac’s Ph.D. thesis was all about his additions and developments on Heisenberg’s theory. In a few years he published a groundbreaking equation, one that would do something that had never been done before. He discovered a wave equation that incorporated both special relativity and quantum mechanics. We now call this equation the Dirac equation and it helps us study the motion and spin of electrons. This event kicked off the discovery of QED.
Along with helping in the creation of QED, in the 1940’s and ‘50s Feynman created a tool that has helped us visually explain particle interactions. He created the Feynman Diagrams. In quantum electrodynamics it helps us to visualize and calculate interactions between electrons and photons.
The Dirac equation was discovered in 1928 and in the late 1940’s three scientists, Richard Feynman, Julian Schwinger, and Tomonaga Shin’ichirō, independently built a quantum theory of electromagnetism with the help of his equation. There were some faults in Dirac’s equation so all of these scientists found different ways to look at the problem so that they could solve it. They were awarded a shared Nobel Prize.
Mathematics
The Dirac equation (see Figure 1) laid the ground for QED. Its main purpose is to explain the spin of electrons. He said that spin emerged as a property of an electron, a property that is both a quantum particle and a relativistic one. His equation also predicted the positron, what Dirac called the “anti-electron”. If an electron meets a positron the two positive and negative charges cancel, the pair annihilates, and the mass turns into radiation, an exact representation of Einstein’s E = mc2. The equation has four wave functions.
Julian Schwinger was a participant of a meeting where data was presented that contradicted Dirac’s equation. From there Schwinger made a calculation that incorporated notions of mass and charge re-normalization, a calculation that connected both theory and experimental data. This breakthrough was vital. Tomonaga Shin’ichirō and Richard Feynman also discovered and carried out calculations similar to this and in 1965 all three of them shared a Nobel Prize.
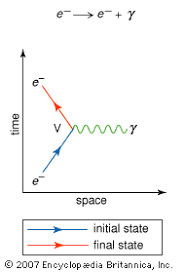
A Feynman diagram has one axis that represents space, the horizontal one, and the other axis, this one being vertical, represents time. Straight lines depict fermions–particles with half-integer values of spin, like electrons–and wavy lines represent bosons–particles that have integer values of spin, like photons. An interaction of particles is shown as a vertex of three lines. For example, the path of a basic electron as two straight lines intersected with a wavy line where the electron emits a photon (see Figure 2).
Applications
The most notable use of quantum electrodynamics is to explain the world around us. It helps us understand how light and matter interact, and how electrically charged particles interact with each other. It is a widely taught subject as the joining of classical and quantum is our future and many other quantum field theories have been modeled after QED.
If we dissect the elements of QED then each of them have various other uses like, for example, the Dirac equation also helps scientists predict the existence of antiparticles. Like mentioned before the Feynman diagrams help explain all particle interactions and along with that give physicists a way to make very precise calculations on the probability of any process.
Conclusion
Quantum electrodynamics is an amazing tool to help us look at and understand the world in a new way. It shows us that electrons and positrons–or any other charged particle–interact by emitting and absorbing photons. It is one of the most successful, simple and accurate quantum field theory so far devised. It is clear that quantum electrodynamics is a vital part of quantum physics.